Imagine, A time traveler in the present time steals a time machine from a museum to make his time trip and travel back in time; he travels back in time and reaches the past, then at the end of the journey, he donates the time machine to the same museum from where he stole it. In this case, the time machine is never built by anyone; it simply exists. So what is the reason behind the existence of the Time Machine without the origin?
Thus, time traveling in the past would allow for the possibility of causal loops, in which things come from nowhere to arrive or emerge unexpectedly. Things here might be events, information, people, or objects. In this article, we have briefly discussed what a causal loop is and what is a causal loop’s significance in time travel.
Contents
- 1 What is a Causal loop?
- 2 Nomenclature Causal loop
- 3 Causal Loops and Multi-Dimensional Time
- 4 Quantum computation with negative delay
- 5 Self-fulfilling prophecy
- 6 Novikov self-consistency principle
- 7 Conclusion and Final thoughts
- 8 Sources
What is a Causal loop?
The causal loop is a theoretical proposition of either retro-causality or a simple paradox of time travel that occurs when a future event is the cause of a past event, which in turn is the cause of the coming event. In other words, a sequence of events, such as actions, information, objects, or people, is among the reasons for another possibility, which is, in turn, among the causes of the first-mentioned event. Such causally looped circumstances exist in Spacetime, but their origin cannot be determined. This means it cannot be told what is or was the origin of a causal loop.
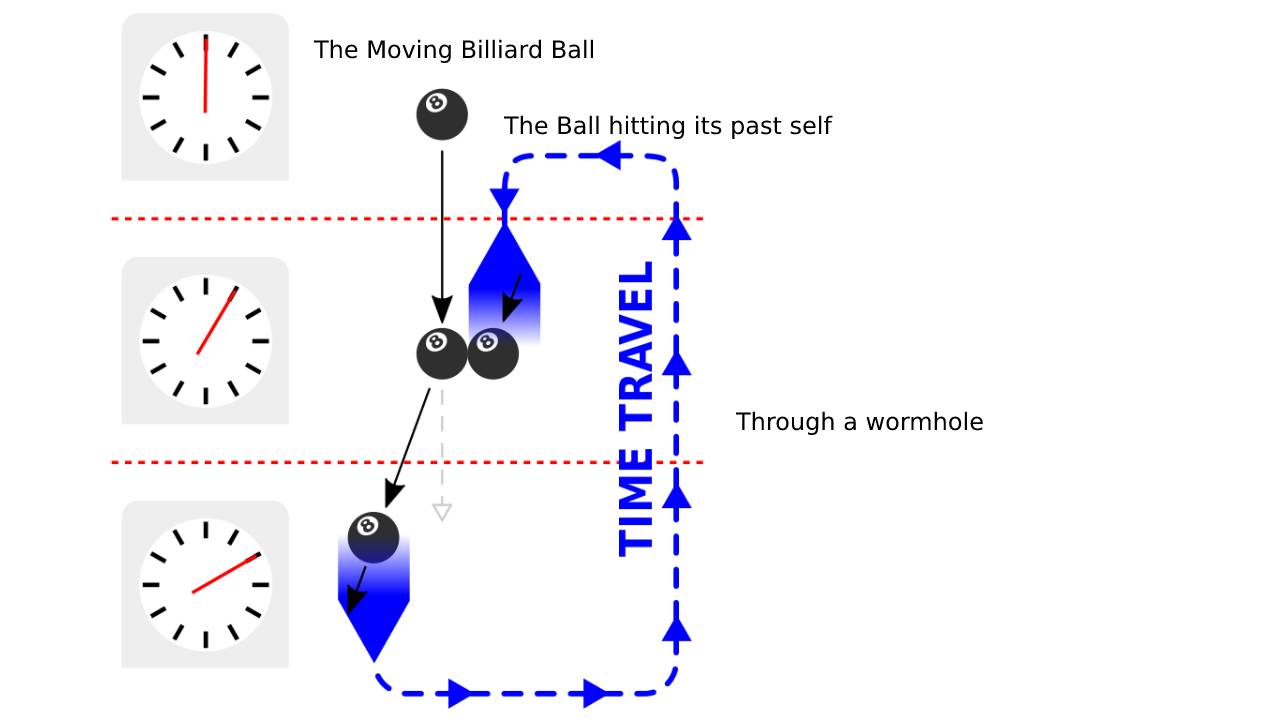
A most popular hypothetical example of a causality loop is given a billiard ball striking its past self. Below is the diagram of a causal loop illustrated with a billiard ball. Top: original billiard ball trajectory. Middle: the billiard ball emerges from the future at a different angle than the original and delivers its past self a glancing blow. Bottom: the billiard ball changed its trajectory just the right way so it would travel back in time with the angle required to deliver the glancing blow to its younger self.
The above diagram of a causal loop is illustrated with a billiard ball. Top: original billiard ball trajectory. Middle: the billiard ball emerges from the future at a different angle than the original and delivers its past self a glancing blow. Bottom: the billiard ball changed its trajectory just the right way so it would travel back in time with the angle required to deliver the glancing blow to its younger self.
The billiard ball moves in a path toward a time machine. The future self of the billiard ball emerges from the time machine before its past self enters it, giving its past self a glancing blow, altering the past ball’s path and causing it to enter the time machine at an angle that would cause its future self to strike its past self the very glancing blow that altered its path. In this sequence of events, the change in the ball’s path is its cause, which might appear paradoxical.
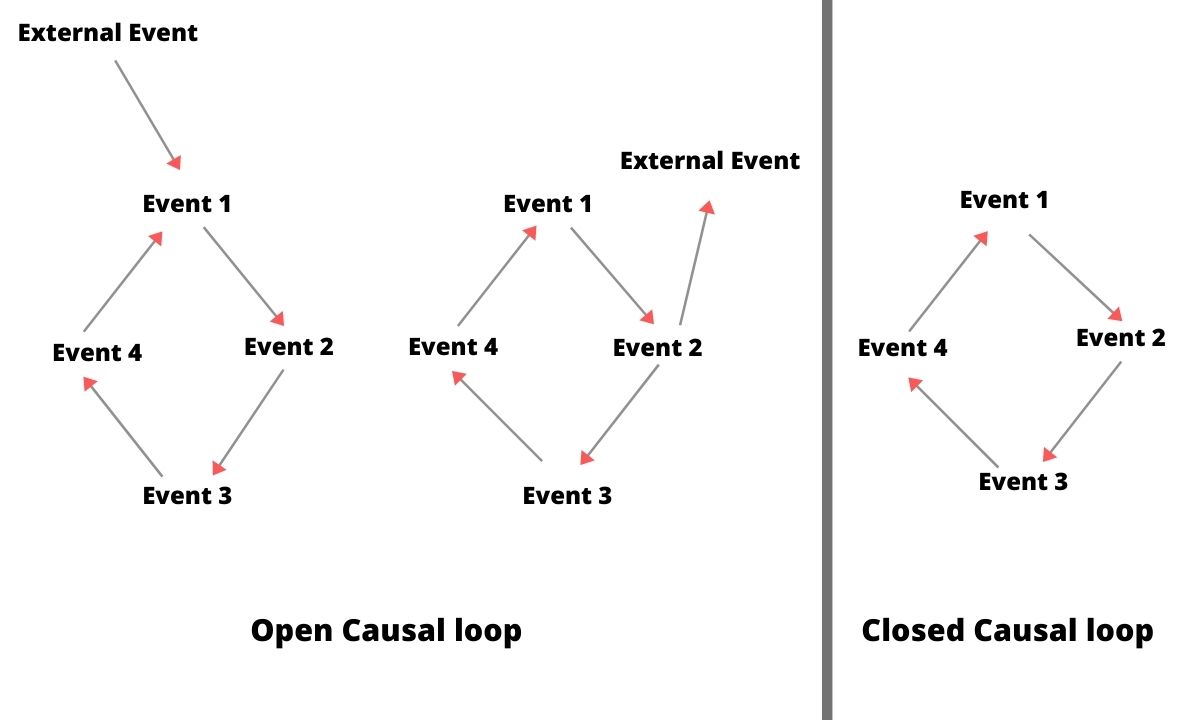
Thus we can say that the causal loop is a sequence of events e1, …, en. Each event in the loop is one of the causes of the next event. The last event, en, is one of the causes of the first event, e1. If a causal loop has no external (outside-the-loop) causes or effects, then that causal loop is a closed causal loop; otherwise, it is an open causal loop. Think of closed causal loops as causally isolated. Think of open causal loops as causally embedded. See the diagram below.
Two kinds of Casual loops
Examples of a Causal loop Paradox
Allan Everett has given an example of a causal loop paradox involving information: suppose a time traveler copies a mathematical proof from a textbook, then travels back to meet the mathematician who first published the evidence at a date before publication and allows the mathematician to copy the proof. In this case, the information in the evidence has no origin.
A similar example is given in the television series “Doctor Who” of a hypothetical time-traveler who copies Beethoven’s music from the future and publishes it in Beethoven’s time in Beethoven’s name. Finally, Everett gives the movie Somewhere in Time as an example involving an object with no origin: an older woman gives a watch to a playwright who later travels back in time and meets the same woman when she was young and gives her the same look that she will later give to him.
Krasnikov writes that these bootstrap paradoxes (information or an object looping through time) and simple loop are the same; the primary apparent contradiction is a physical system evolving into a state in a way that is not governed by its laws. However, he does not find this paradoxical and attributes problems regarding the validity of time travel to other factors in interpreting general relativity.
Nomenclature Causal loop
Traveling back in time would allow for causal loops, which include events, information, people, or objects whose histories form a closed loop and thus seem to arrive or emerge unexpectedly. The notion of objects or information that are “self-existing” in this way is often viewed as paradoxical, and several authors refer to this a Causal loop that involves information or objects without origin as a Bootstrap paradox, an information paradox, or an ontological paradox (Ontology means the branch of metaphysics dealing with the study of being and existence)
The term time loop is sometimes referred to as a causal loop, but although they appear similar, causal loops are unchanging and self-originating, whereas time loops are constantly resetting.
The term “bootstrap” here refers to the expression “pulling yourself up by your bootstraps.” Learn more about Bootstrap Paradox here: Bootstrap Paradox, a theoretical paradox of time travel. You can also read Robert A. Heinlein’s time travel story “By His Bootstraps” (PDF).
The term Causal loop in Science fiction movies, books, and philosophies
In a 1992 paper, Physicists Andrei Lossev and Igor Novikov labeled such sequence of events (actions, information, objects, people) without origin as Jinn, with the singular term Jinnee. This terminology was inspired by the Jinn of the Quran, which is described as leaving no trace when they disappear. Lossev and Novikov allowed the term “Jinn” to cover both objects and information with the reflexive origin; they called the former “Jinn of the first kind” and the latter “Jinn of the second kind.”
They point out that an object making a circular path through time must be identical whenever it is brought back to the past. Otherwise, it would create an inconsistency. According to the second law of thermodynamics, the object becomes more disordered throughout its history. Such objects that are identical in repeating points in their history seem to contradict this. Still, Lossev and Novikov argued that since the second law only requires disorder to increase in closed systems, a Jinnee could interact with its environment in such a way as to regain lost order. They emphasize that there is no “strict difference” between the first and second kind. Krasnikov equivocates between “Jinn,” “self-sufficient loops,” and “self-existing objects,” calling them “lions” or “looping or intruding objects,” and asserts that they are no less physical than conventional objects, “which, after all, also could appear only from either infinity or a singularity.”
An example of a Jinni is Swann’s necklace from the 1982 film Timerider: The Adventure of Lyle Swann.
In the 1982 film Timerider: The Adventure of Lyle Swann., Motorcycle racer Lyle Swann accidentally falls into a time-travel experiment and finds himself transported back to the Old West of the 1870s. There he meets a woman named Claire, who eventually attracts him. After a series of spectacular events, the people who accidentally transported him back in time try to rescue him by sending a helicopter but just before Swann is saved, Claire snatches a necklace from Swann that was given to Swann by his great-great-grandmother who stole it from his great-great-grandfather. The chain is a jinni because Swann receives the necklace from his great-great-grandmother, who stole the same necklace from him years earlier. You might think here that Claire is Swann’s great-great-grandma. However, Swann himself is his great-great-grandpa.
Here this problem raises many questions presented by the necklace. How can a physical object like a necklace without origin exist? Who designed the necklace? What explains why it is a necklace rather than a bracelet? There must be some explanation for why the chain is the way it is. What is the origin? These questions might come into our minds.
There are explanations for the stages of the necklace’s existence. The chain has caused. Swann’s receiving the chain from his grandmother is a cause of him taking it with him back in time. The necklace’s going back in time is a cause of Claire being able to steal the chain, and so on. In addition, one could argue that the Universe and natural laws must have a specific structure for causal loops to exist. These laws would also be a source of practical explanations.
Some facts, though, seem bound to go unexplained, like the necklace is a necklace, not a bracelet. In addition, Why is there a loop without an origin? Why is there a causal loop rather than no causal loop? Does our inability to explain these facts show that there is something incoherent about causal loops? The problem with this reasoning is that similar issues arise regarding everyday objects. You can see the causes of a chair because the carpenter built the chair from wood, but what made the wood? Even more so, what made the atoms that compose the wood? One can keep asking these questions, There may be entirely adequate and complete explanations of these, but it is impossible to proceed under normal circumstances. We may never get a good reason for many facts and things.
Here also, in the case of the necklace, consider the origin of the artistic design of the chain. The necklace appeared to be expected, one that had been crafted with intent and artistry. However, this begs the question of where artistry came from. Who’s (or what’s) skill and knowledge went into creating this necklace? Storrs McCall (2010) says there is no solution to this problem. Perhaps, some facts do not have explanations. However, insisting that everything must have an answer is unwarranted.
Predestination paradox
Another example from Star Trek is where the predestination paradox is used to mean “a time loop in which a time traveler who has gone into the past causes an event that ultimately causes the original future version of the person to go back into the past.” This use of the phrase was created for a sequence in a 1996 episode of Star Trek: Deep Space Nine titled “Trials and Tribble-ations.” This phrase had also been used previously to refer to belief systems such as Calvinism and some forms of Marxism that encouraged followers to strive to produce specific outcomes while at the same time teaching that the results were predetermined. Smeenk and Morgenstern use the term “predestination paradox” to refer specifically to situations in which a time traveler goes back in time to try to prevent some event in the past but ends up helping to cause that same event.
The term Causal loop in Physics
To introduce some theoretical causal loops in physics, let us consider the idea of a timelike curve. A timelike curve is an object’s path through Spacetime where the thing persists locally forward in time with timelike connections between intervals. A causal loop occurs when an object’s timelike curve loops back on itself.
One way of introducing a causal loop is with the idea that the Universe has a rolled-up spacetime. The best analogy for this idea is a cylinder where the dimensions that makeup space are the cylinder’s axis. This structure allows an object’s timelike curve to loop around the cylinder and meet up with itself.
The above image is explained when Einstein presented the world with a new understanding of the world- his theory of general relativity. In this theory, space is not an empty void but an invisible structure called Spacetime. Nor is space simply a three-dimensional grid through which matter and energy move. It is a four-dimensional structure whose shape is determined by the presence of matter and energy. Around any mass (or energy), Spacetime is curved. The presence of planets, stars, and galaxies deforms the fabric of Spacetime like a giant ball bends a bedsheet. (This deformation occurs in four dimensions, so the two-dimensional bedsheet is a limited model. Try visualizing these depressions on all sides of a planet to build a more accurate image of this concept.) When a smaller mass passes near a larger group, it curves toward the larger group because Spacetime is bent toward the larger mass. The smaller pack is not “attracted” to the larger mass by force. Instead, the smaller mass follows the structure of curved Spacetime near the larger group. For example, the massive Sun curves spacetime around it, a curvature that reaches out to the edges of the solar system and beyond. The planets orbiting the Sun are not being pulled by the Sun; they are following the curved Spacetime deformed by the Sun.
Wormhole-based time travel also allows for closed timelike curves; Physics poses some serious problems for the possibility of Jinn (discussed above). According to the second law of thermodynamics, entropy (or disorder) always increases with time. Consider the example of the necklace in Timerider.
According to thermodynamics
Under normal circumstances, the entropy of the necklace (discussed above) would increase from when Claire stole the necklace to when the chain was given to Swan and until Swan did time travel. Now, most understandings of time travel do not change the position of objects as they travel back in time. Since the entropy of defeat just before Swan returns must have the same amount as if Swan comes past, this would create a contradiction. Since the entropy of loss just before Swan goes back must have the same amount as Swan coming past, this would make a contradiction because the entropy of defeat just before Swan left is equal to Swan coming past and happens more. This Paradox means that for the Genie to exist, the time travel model must account for some way of reducing the entropy to return to the past.
Rather than originating from a big bang, the Universe began as a spacetime ‘doughnut.’
Another exciting example of causal loops in physics is the hypothesis that, rather than originating from a big bang, the Universe began as a spacetime ‘doughnut’ from which the rest of the Universe branched—the authors of this theory, J. Richard Gott and Li-Xin Li formulated this theory using an alternative solution to Einstein’s field equations. The spacetime doughnut is a causal loop with closed and open paths around the circle. So, in some ways, Spacetime exists as a loop, but others branch off to make the rest of the Universe and its contents.
Causal Loops and Multi-Dimensional Time
Multi-Dimensional time is sometimes called the structure of time with the branching of timelines, removing most of the exciting features of causal loops. It is sometimes introduced to keep causal loops out. Time-traveling causes timelines to split with multi-dimensional time, so an event cannot cause an event along its past branch. This unwraps the circles, and a series of split causal chains are left. A result of this is that if multi-dimensional time were to be accurate, then the answer to whether time travel to the past always involves a causal loop would be a no. This is because a time traveler creates branches instead of circles.
Quantum computation with negative delay
In a 1991 paper, Physicist David Deutsch showed that quantum computation with a negative delay (backward time travel) could solve NP problems in polynomial time. Later Scott Aaronson extended this result to show that the model could also solve PSPACE problems in polynomial time. However, Deutsch showed that quantum computation with a negative delay produces only self-consistent solutions, and the chronology-violating region imposes constraints that are not apparent through classical reasoning. In 2014 Researchers published a simulation validating Deutsch’s model with photons. However, it was shown in an article by Tolksdorf and Verch that Deutsch’s CTC (closed timelike curve, or a causal loop) fixed-point condition can be fulfilled to arbitrary precision in any quantum system described according to relativistic quantum field theory on spacetimes where CTCs are excluded, casting doubts on whether Deutsch’s condition is characteristic of quantum processes mimicking CTCs in the sense of general relativity.
Self-fulfilling prophecy
A self-fulfilling prophecy is a process in which an initially false expectation leads to its confirmation. In a self-fulfilling prophecy, an individual’s expectations about another person or entity eventually result in the other person or entity acting in ways that confirm the expectations.
Thus self-fulfilling prophecy may be a form of causality loop. Predestination does not necessarily involve a supernatural power and could result from other “infallible foreknowledge” mechanisms. Newcomb’s Paradox explores problems arising from infallibility and influencing the future. A notable fictional example of a self-fulfilling prophecy occurs in the classical play Oedipus Rex, in which Oedipus becomes the king of Thebes and unwittingly fulfills a prophecy that he will kill his father and marry his mother. The prophecy itself is the impetus for his actions, and thus it is self-fulfilling. The movie 12 Monkeys heavily deals with themes of predestination and the Cassandra complex, where the protagonist who travels back in time explains that he can’t change the past.
Novikov self-consistency principle
General relativity permits some exact solutions that allow for time travel. Some of these accurate solutions describe universes that contain closed timelike curves or world lines that lead back to the same point in Spacetime. Physicist Igor Dmitriyevich Novikov discussed the possibility of closed timelike curves in his books in 1975 and 1983, offering the opinion that only self-consistent trips back in time would be permitted. A 1990 paper, “Cauchy problem in spacetimes with closed timelike curves,” by Novikov and several others, suggests the principle of self-consistency, which states that only solutions to the laws of physics that can occur locally in the real Universe are those which are globally self-consistent. The authors later concluded that time travel need not lead to unresolvable paradoxes, regardless of what type of object was sent to the past.
Physicist Joseph Polchinski argued that one could avoid questions of free will by considering a paradoxical situation involving a billiard ball sent back in time. In this situation, the ball is fired into a wormhole at an angle such that, if it continues along its course, it will exit in the past at just the right angle to hit its earlier self, knocking it off course, which would stop it from entering the wormhole in the first place. Thorne referred to this problem as “Polchinski’s paradox.” Two students at Caltech, Fernando Echeverria, and Gunnar Klinkhammer, went on to find a solution that avoided any inconsistencies.
In the revised scenario, the ball would emerge from the future at a different angle than the one that had generated the Paradox and delivers its past self a glancing blow instead of knocking it entirely away from the wormhole. This blow changes its trajectory by just the right degree, meaning it will travel back in time with the angle required to deliver its younger self the necessary glancing blow. Echeverria and Klinkhammer found more than one self-consistent solution, with slightly different tips for the glancing impact in each case. Later analysis by Thorne and Robert Forward showed that there could be an infinite number of self-consistent solutions for specific initial trajectories of the billiard ball.
Echeverria, Klinkhammer, and Thorne published a paper discussing these results in 1991. They also reported that they had tried to see if they could find any initial conditions for the billiard ball for which there were no self-consistent extensions but were unable to do so. Thus it is plausible that self-consistent extensions exist for every possible initial trajectory, although this has not been proven. The lack of constraints on initial conditions only applies to Spacetime outside the chronology-violating region; the rules on the chronology-violating part might prove to be paradoxical, but this is not yet known.
Novikov’s views are not widely accepted. For example, Visser views causal loops and Novikov’s self-consistency principle as an ad hoc solution and supposes that time travel has far more damaging implications. Krasnikov similarly finds no inherent fault in causal loops but finds other problems with time travel in general relativity.
Conclusion and Final thoughts
At the beginning of this article, we have discussed a time traveler who steals a time machine from a museum to make his time trip; he travels back in time and reaches the past, then at the end of the journey, he donates the time machine to the same museum from where he stole it. Here we can examine some aspects of this Paradox intensely, but we may have many questions, too, so the discussion is always open. Can you find out where the time machine came from despite these questions? You can’t, and we too can’t because here, the time machine is never built by anyone – it simply exists. This time traveling in the past would allow for Causal loops, in which things come from nowhere to arrive or emerge unexpectedly.
Sources
- Meyer, Ulrich. “Explaining Causal Loops.” Analysis 72 (2012): 259-264.
- Smith, Nicholas J.J. (2013). “Time Travel.” Stanford Encyclopedia of Philosophy. Retrieved June 13, 2015.
- Rea, Michael C. (2009). Arguing about Metaphysics. New York [u.a.]: Routledge. p. 204. ISBN 978-0-415-95826-4.
- Thorne, Kip S. (1994). Black Holes and Time Warps. W. W. Norton. pp. 509–513. ISBN 0-393-31276-3.
- Everett, Allen; Roman, Thomas (2012). Time Travel and Warp Drives. Chicago: University of Chicago Press. pp. 136–139. ISBN 978-0-226-22498-5.
- Smeenk, Chris; Wüthrich, Christian (2011), “Time Travel and Time Machines”, in Callender, Craig (ed.), The Oxford Handbook of Philosophy of Time, Oxford University Press, p. 581, ISBN 978-0-19-929820-4
- Ross, Kelley L. (1997). “Time Travel Paradoxes”. Archived from the original on January 18, 1998.
- Jones, Matthew; Ormrod, Joan (2015). Time Travel in Popular Media. McFarland & Company. p. 207. ISBN 9780786478071.
- Holmes, Jonathan (October 10, 2015). “Doctor Who: what is the Bootstrap Paradox?”. Radio Times.
- Krasnikov, S. (2001), “The time travel paradox”, Phys. Rev. D, 65 (6): 06401, arXiv:gr-QC/0109029, Bibcode:2002PhRvD..65f4013K, DOI:10.1103/PhysRevD.65.064013
- Lossev, Andrei; Novikov, Igor (15 May 1992). “The Jinn of the time machine: non-trivial self-consistent solutions” (PDF). Class. Quantum Gravity. 9 (10): 2309–2321. Bibcode:1992CQGra…9.2309L. DOI:10.1088/0264-9381/9/10/014. Archived from the original (PDF) on November 17, 2015. We retrieved November 16, 2015.
- Okuda, Michael; Okuda, Denise (1999). The Star Trek Encyclopedia. Pocket Books. p. 384. ISBN 0-671-53609-5.
- Erdmann, Terry J.; Hutzel, Gary (2001). Star Trek: The Magic of Tribbles. Pocket Books. p. 31. ISBN 0-7434-4623-2.
- Daniels, Robert V. (May–June 1960). “Soviet Power and Marxist Determinism.” Problems of Communism. 9: 17.
- Deutsch, David (1991). “Quantum mechanics near closed timelike lines.” Physical Review D. 44 (10): 3197–3217. Bibcode:1991PhRvD..44.3197D. DOI:10.1103/PhysRevD.44.3197. PMID 10013776.
- Aaronson, Scott (March 2008). “The Limits of Quantum Computers” (PDF). Scientific American. 298 (3): 68–69. Bibcode:2008SciAm.298c..62A. DOI:10.1038/scientificamerican0308-62.
- Martin Ringbauer; Matthew A. Broome; Casey R. Myers; Andrew G. White; Timothy C. Ralph (June 19, 2014). “Experimental simulation of closed timelike curves.” Nature Communications. 5: 4145. arXiv:1501.05014. Bibcode:2014NatCo…5.4145R. DOI:10.1038/ncomms5145. PMID 24942489.
- Tolksdorf, Juergen; Verch, Rainer (2018). “Quantum physics, fields and closed timelike curves: The D-CTC condition in quantum field theory.” Communications in Mathematical Physics. 357 (1): 319–351. arXiv:1609.01496. Bibcode:2018CMaPh.357..319T. DOI:10.1007/s00220-017-2943-5.
- Craig, William Lane (1987). “Divine Foreknowledge and Newcomb’s Paradox.” Philosophia. 17 (3): 331–350. DOI:10.1007/BF02455055.
- Dummett, Michael (1996). The Seas of Language. Oxford University Press. pp. 356, 370–375. ISBN 9780198240112.
- Dodds, E.R. (1966), Greece & Rome 2nd Ser., Vol. 13, No. 1, pp. 37–49
- Krasnikov, S. (2002), “No time machines in classical general relativity,” Classical and Quantum Gravity, 19 (15): 4109, arXiv:gr-QC/0111054, Bibcode:2002CQGra..19.4109K, DOI:10.1088/0264-9381/19/15/316
- Carroll, Sean (2004). Spacetime and Geometry. Addison Wesley. ISBN 0-8053-8732-3.
- Friedman, John; Morris, Michael S.; Novikov, Igor D.; Echeverria, Fernando; Klinkhammer, Gunnar; Thorne, Kip S.; Yurtsever, Ulvi (1990). “Cauchy problem in spacetimes with closed timelike curves.” Physical Review D. 42 (6): 1915. Bibcode:1990PhRvD..42.1915F. DOI:10.1103/PhysRevD.42.1915. PMID 10013039.
- Novikov, Igor (1983). Evolution of the Universe, p. 169: “The close of time curves does not necessarily imply a violation of causality, since the events along such a closed line may be all ‘self-adjusted’—they all affect one another through the closed cycle and follow one another in a self-consistent way.”
- Echeverria, Fernando; Gunnar Klinkhammer; Kip Thorne (1991). “Billiard balls in wormhole spacetimes with closed timelike curves: Classical theory.” Physical Review D. 44 (4): 1077. Bibcode:1991PhRvD..44.1077E. DOI:10.1103/PhysRevD.44.1077.
- Earman, John (1995). Bangs, Crunches, Whimpers, and Shrieks: Singularities and Acausalities in Relativistic Spacetimes. Oxford University Press. ISBN 0-19-509591-X.
- Nahin, Paul J. (1999). Time Machines: Time Travel in Physics, Metaphysics, and Science Fiction. American Institute of Physics. pp. 345–352. ISBN 0-387-98571-9.
FACT CHECK: We strive for accuracy and fairness. But if you see something that doesn’t look right, please Contact us.
DISCLOSURE: This Article may contain affiliate links and Sponsored ads, to know more please read our Privacy Policy.
Stay Updated: Follow our WhatsApp Channel and Telegram Channel.