कल्पना कीजिए, वर्तमान समय में एक समय यात्री समय यात्रा करके समय में पीछे जाने के लिए एक संग्रहालय से एक टाइम मशीन चुराता है, वह समय यात्रा करता है और अतीत में पहुंचता है, फिर यात्रा के अंत में वह टाइम मशीन उसी संग्रहालय में दान कर देता है जहां से उसने उसे वर्तमान समय में चुराया था। इस मामले में टाइम मशीन खुद कभी किसी के द्वारा बनाई नहीं गई है, यह बस मौजूद है। टाइम मशीन के बिना मूल(origin) के मौजूद होने के पीछे कारण क्या है यह एक प्रश्न है।
इस प्रकार अतीत में यात्रा करने से कारणीय लूप (कॉज़ल लूप – Causal loop) की संभावना उत्पन्न होती है, जिसमें चीजें स्पेस टाइम मे अप्रत्याशित रूप से बस मौजूद हैं जिसका मूल(origin) किसी को नहीं पता। यहां चीजें घटना, सूचना, लोग या वस्तुएं हो सकती हैं। इस लेख में हमने संक्षेप में चर्चा की है कि एक कारण लूप (Causal loop) क्या होता है, और समय यात्रा में कारणीय लूप का क्या महत्व है?
Contents
- 1 एक कारण लूप (Causal loop) क्या होता है?
- 2 कारण लूप का नामकरण
- 3 कॉसल लूप्स और मल्टी-डायमेंशनल टाइम
- 4 क्वांटम गणना के साथ नेगेटिव डिले
- 5 स्वयंकार्यान्वित भविष्यवाणी(Self-fulfilling prophecy)
- 6 नोविकोव आत्म-संगति सिद्धांत
- 7 निष्कर्ष और अंतिम विचार
- 8 स्त्रोत
एक कारण लूप (Causal loop) क्या होता है?
कारण लूप या कारणीय लूप (कॉज़ल लूप – Causal loop) रेट्रो-कारणता का एक सैद्धांतिक प्रस्ताव है या समय यात्रा का एक सरल विरोधाभास, जो तब होता है जब कोई भविष्य की घटना अतीत की घटना का कारण होता है, और फिर अतीत बदले में भविष्य की घटना का कारण होता है। दूसरे शब्दों में, क्रियाओं, सूचनाओं, वस्तुओं या लोगों जैसी घटनाओं का एक क्रम किसी अन्य घटना के कारणों में से एक है, जो बदले में पहली घटना के कारणों में से एक है। इस तरह के कारणात्मक रूप से लूप की घटनाएं तब बस स्पेसटाइम में मौजूद होती हैं, लेकिन उनकी उत्पत्ति यानि मूल(origin) निर्धारित नहीं किया जा सकता। इसका मतलब यह नहीं बताया जा सकता कि किसी कारणीय लूप की उत्पत्ति या मूल(origin) क्या है।
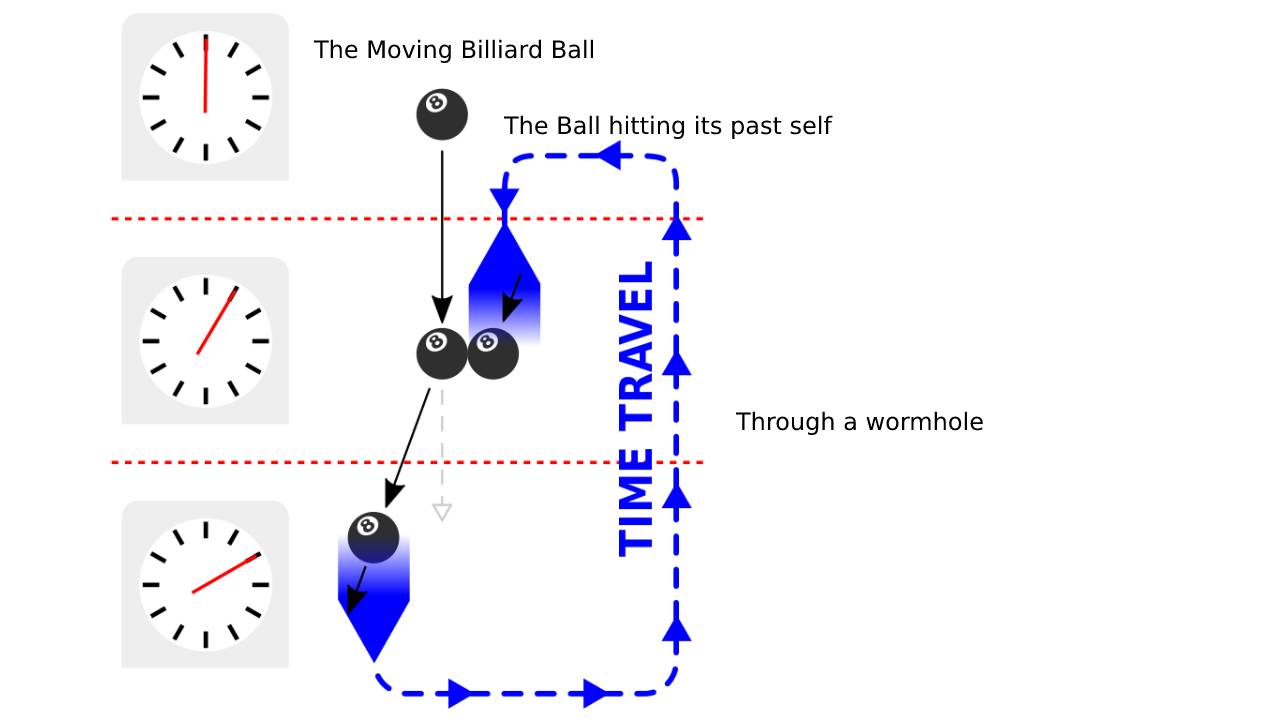
करणीय लूप का सबसे लोकप्रिय काल्पनिक उदाहरण एक बिलियर्ड बॉल का दिया गया है, जो अपने पिछले स्वयं से टकराता है जिसे एक बिलियर्ड बॉल के साथ नीचे चित्रित किया गया है। सबसे ऊपर: मूल बिलियर्ड बॉल प्रक्षेपवक्र(trajectory), मध्य मे: बिलियर्ड बॉल मूल की तुलना में एक अलग कोण पर भविष्य से उभरता है, और अपने पिछले स्वयं से टकराता है। नीचे: बिलियर्ड बॉल अपने प्रक्षेपवक्र को दाईं तरफ बदल देता है ताकि यह अपने युवा स्वयं से टकराने के लिए आवश्यक कोण के साथ समय मे पीछे यात्रा करे।
ऊपर एक बिलियर्ड लूप का आरेख है जिसे एक बिलियर्ड बॉल के साथ चित्रित किया गया है। सबसे ऊपर: मूल बिलियर्ड बॉल प्रक्षेपवक्र(trajectory) । मध्य मे: बिलियर्ड बॉल मूल की तुलना में एक अलग कोण पर भविष्य से उभरता है, और अपने पिछले स्वयं से टकराता है। नीचे: बिलियर्ड बॉल अपने प्रक्षेपवक्र को दाईं तरफ से बदल देता है ताकि यह अपने युवा स्वं से टकराने के लिए आवश्यक कोण के साथ समय मे पीछे यात्रा करे।
बिलियर्ड बॉल एक पथ पर टाइम मशीन की ओर जाता है, और भविष्य का बिलियर्ड बॉल टाइम मशीन से निकलता है, इससे पहले कि उसका अतीत का स्वयं उसमें प्रवेश कर जाए, इससे वह अपने अतीत के स्वयं के मार्ग को बदल देता है और उसे टाइम मशीन में प्रवेश करने के लिए प्रेरित करता है, एक ऐसे कोण पर जो उसके भविष्य के स्वयं को उसके अतीत के स्वयं से टकराने के लिए प्रेरित करेगा, वही टकराव जिसने उसका मार्ग बदल दिया था। घटनाओं के इस क्रम में गेंद के मार्ग में परिवर्तन का अपना कारण है, जो विरोधाभासी दिखाई दे सकता है।
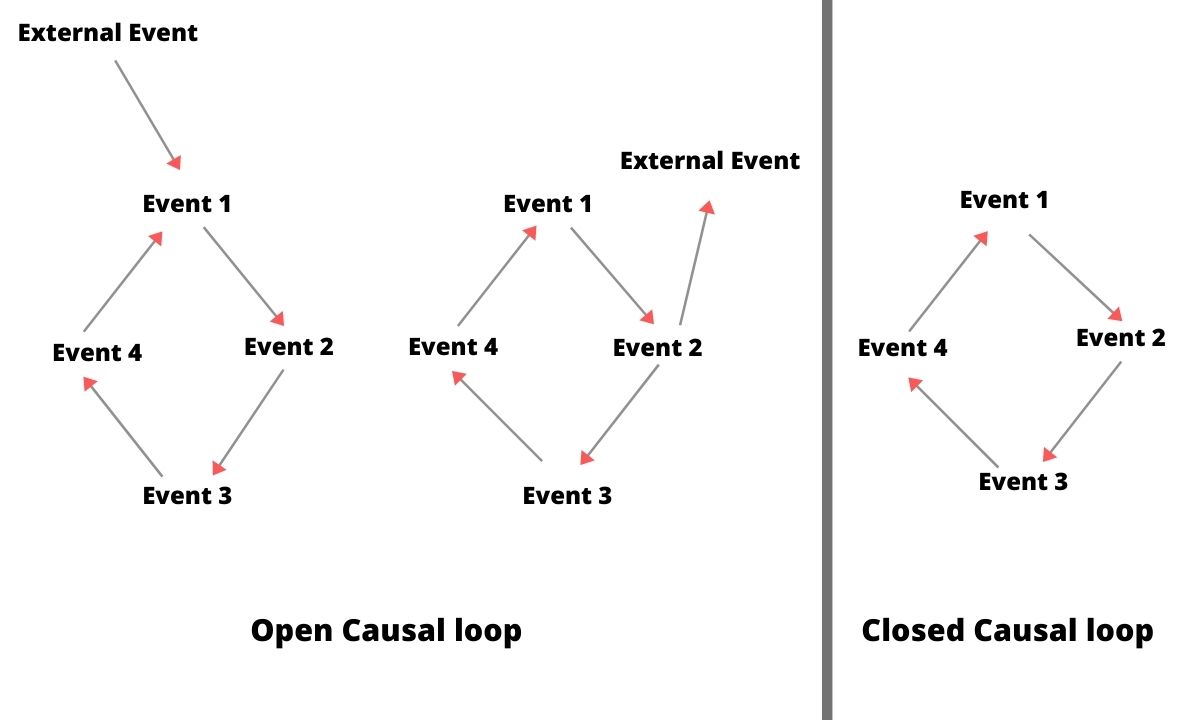
इस प्रकार हम कह सकते हैं कि कारण लूप घटनाओं e1,…, en का एक क्रम है। लूप की प्रत्येक घटना अगले ईवेंट के कारणों में से एक है। अंतिम ईवेंट en पहली ईवेंट e1 के कारणों में से एक है। यदि एक कारण लूप का कोई बाहरी (बाहर का लूप) कारण या प्रभाव नहीं है, तो वह कारण लूप एक बंद कारण लूप है; अन्यथा, यह एक खुला कारण लूप है। बंद करणीय छोरों को यथोचित अलग-थलग समझें। खुले रूप में कारण के रूप में एम्बेडेड छोरों के बारे में सोचें। नीचे चित्र देखें।
दो प्रकार के कारण लूप
कारण लूप विरोधाभास के उदाहरण
एलन एवरेट(Allan Everett) ने कारण लूप विरोधाभास का एक उदाहरण दिया है जिसमें जानकारी शामिल है: मान लें कि एक यात्री एक पाठ्यपुस्तक से एक गणितीय प्रमाण की प्रतिलिपि कॉपी करता है, और इस पाठ्यपुस्तक के गणितज्ञ लेखक जिसने पहले प्रमाण प्रकाशित किया था, से मिलने के लिए समय में पीछे यात्रा करता है, और प्रकाशन से पहले गणितज्ञ को प्रमाण की नकल करने अनुमति देता हैं। इस मामले में, पाठ्यपुस्तक के गणितीय प्रमाण में जानकारी का कोई मूल यानि स्रोत नहीं है।
इसी तरह का एक उदाहरण एक काल्पनिक समय-यात्री की टेलीविज़न श्रृंखला “डॉक्टर हू” में दिया गया है जो बीथोवेन के संगीत को भविष्य से कॉपी करता है और इसे बीथोवेन के समय में बीथोवेन के नाम से प्रकाशित करता है। एवरेट फिल्म को समय में कहीं पर एक उदाहरण के रूप में देता है जिसमें कोई मूल के साथ एक वस्तु शामिल है: एक बूढ़ी महिला एक नाटककार को घड़ी देती है फिर नाटककार बाद में समय यात्रा करके समय मे पीछे जाता है और उसी महिला से मिलता है जब वह छोटी थी और उसे वही घड़ी देता है जिसे वह महिला भविष्य मे जब वह बूढ़ी होगी तब फिर से उस नाटककार को वापस कर देगी।
कर्सनिकोव लिखते हैं कि ये बूटस्ट्रैप विरोधाभास (समय के माध्यम से सूचना या एक वस्तु लूपिंग) और कारण लूप एक ही है; प्राथमिक स्पष्ट विरोधाभास एक भौतिक प्रणाली है जो किसी रूप में इस तरह से विकसित होती है की यह अपने ही कानूनों द्वारा नियंत्रित न हो। कर्सनिकोव इन्हे विरोधाभास नहीं मानते, बल्कि सामान्य सापेक्षता की व्याख्या में अन्य कारकों के लिए समय यात्रा की वैधता के बारे में समस्याओं का वर्णन करते हैं।
कारण लूप का नामकरण
समय में पीछे यात्रा करने से कारण लूपों की परिस्थिति पैदा होती है, जिसमें घटनाओं, सूचनाओं, लोगों या वस्तुओं को शामिल किया जाता है जिनके इतिहास एक बंद लूप बनाते हैं, और इस तरह अप्रत्याशित रूप से आने या उभरने लगते हैं। इस तरह से “स्व-मौजूदा” वस्तुओं या सूचनाओं की धारणा को अक्सर विरोधाभास के रूप में देखा जाता है, और कई लेखक इस परिस्थिति को कारण लूप कहते हैं जिसमें बूटस्ट्रैप विरोधाभास, सूचना विरोधाभास, या एक सत्तामूलक(ontological) विरोधाभास के रूप में मूल के बिना जानकारी या ऑब्जेक्ट शामिल होते हैं। (ओंटोलॉजी का अर्थ है अस्तित्व और अस्तित्व के अध्ययन से निपटने वाले तत्वमीमांसा(metaphysics) की शाखा)
समय लूप को कभी-कभी एक कारण लूप के रूप में संदर्भित किया जाता है, लेकिन यद्यपि वे समान दिखाई देते हैं इसलिए कारण लूप अपरिवर्तनीय और स्व-उत्पत्तित हैं, जबकि समय लूप लगातार रीसेट हो रहे हैं।
यहाँ शब्द “बूटस्ट्रैप” का अर्थ “अपने बूटस्ट्रैप्स द्वारा खुद को ऊपर खींचना” है। बूटस्ट्रैप विरोधाभास के बारे में अधिक जानें यहां: बूटस्ट्रैप विरोधाभास, समय यात्रा का एक सैद्धांतिक विरोधाभास। आप रॉबर्ट ए. हेनलेन की समय यात्रा कहानी “बाय हिज़ बूटस्ट्रैप्स” (पीडीएफ) भी पढ़ सकते हैं।
साइंस फिक्शन फिल्मों, किताबों और दर्शन में कारण लूप (Causal loop) शब्द
1992 के एक पत्र में भौतिकविदों आंद्रेई लॉससेव और इगोर नोविकोव ने इस तरह के घटनाओं (कार्यों, सूचनाओं, वस्तुओं, लोगों) जो बिना मूल(origin) के हैं को जिन कहा, एकवचन शब्द जिनी। यह शब्दावली कुरान के जिन से प्रेरित थी, जिसे गायब होने पर कोई निशान नहीं छोड़ने के रूप में वर्णित किया गया है। लॉससेव और नोविकोव ने “जिन” शब्द को दोनों वस्तुओं और जानकारी को रिफ्लेक्सिव मूल के साथ कवर किया; उन्होंने पहले को “पहली तरह का जिनी” कहा, और बाद वाले को “दूसरी तरह का जिनी” कहा। वे इंगित करते हैं कि समय के माध्यम से एक गोलाकार पथ बनाने वाली वस्तु समान होनी चाहिए, जब भी इसे अतीत में वापस लाया जाता है, अन्यथा यह एक असंगतता पैदा करेगा।
ऊष्मप्रवैगिकी के दूसरे नियम के अनुसार, वस्तु अपने पूरे इतिहास में अधिक अव्यवस्थित हो जाती है, और ऐसी वस्तुएं जो अपने इतिहास में दोहराए जाने वाले बिंदुओं में समान हैं, इसका खंडन करती प्रतीत होती हैं, लेकिन लोसेव और नोविकोव ने तर्क दिया कि चूंकि दूसरे कानून में केवल बंद प्रणालियों में वृद्धि के लिए विकार की आवश्यकता होती है, एक जिनी अपने पर्यावरण के साथ इस तरह से बातचीत कर सकता है जैसे कि खोई हुई व्यवस्था वापस पाने के लिए।
जिनी का एक उदाहरण 1982 की फिल्म टिमराइडर द एडवेंचर ऑफ लाइल स्वान मे स्वान की हार है।
1982 की फिल्म टाइमरइडर: द एडवेंचर ऑफ लाइल स्वान में, मोटरसाइकिल रेसर लाइल स्वान गलती से एक समय-यात्रा प्रयोग में पड़ जाता है और खुद को 1870 के पुराने पश्चिम में पाता है। वहां उसकी मुलाकात क्लेयर नाम की एक महिला से होती है, जो अंततः उसे आकर्षित करती है। शानदार घटनाओं की एक श्रृंखला के बाद जो लोग गलती से उसे समय मे पीछे ले गए थे, एक हेलीकॉप्टर भेजकर उसे बचाने की कोशिश करते हैं, लेकिन स्वान के बचने से ठीक पहले, क्लेयर स्वान से एक हार छीन लेती है जो स्वान को उसकी परदादी द्वारा दिया गया था, जिन्होंने इसे स्वान के परदादा से चुराया था। हार एक जिन्नी है क्योंकि स्वान को अपनी परदादी से हार मिलती है जिसने सालों पहले उससे वही हार चुराया था। आप यहाँ सोच सकते हैं कि, क्लेयर स्वान की परदादी हैं। स्वान स्वयं उनके परदादा हैं।
यहाँ यह समस्या कई सवाल उठा रही है जो कि जिन्न द्वारा उत्पन्न हुई है। हार जैसे भौतिक वस्तु का अस्तित्व उसके मूल के बिना कैसे हो सकता है? हार किसने डिजाइन किया? क्यों यह कंगन के बजाय एक हार है? हार क्यों है, इसके लिए कुछ स्पष्टीकरण होना चाहिए। इसका मूल(origin) क्या है? ये सवाल हमारे दिमाग में आ सकता है।
हार के अस्तित्व के चरणों के लिए स्पष्टीकरण हैं। हार का कारण है। अपनी दादी से हार प्राप्त करना स्वंय का कारण है कि वह उसे समय मे पीछे ले गए। हार का समय मे जाना क्लेयर का कारण बनता है कि वह हार को चुरा सकती है, और इसी तरह इसके अलावा, कोई यह तर्क दे सकता है कि ब्रह्मांड और प्राकृतिक कानूनों में एक विशिष्ट संरचना होनी चाहिए ताकि कारण लूप मौजूद हो सकें। ये कानून उपयोगी स्पष्टीकरण का एक स्रोत भी होंगे।
हालांकि, कुछ तथ्य अस्पष्टीकृत होने के लिए बाध्य लगते हैं, इस तरह के तथ्य कि हार एक हार है और कंगन नहीं। इसके अलावा, बिना मूल(origin) के कारण लूप क्यों है? क्या इन तथ्यों की व्याख्या करने में हमारी असमर्थता दर्शाती है कि कारण लूप के बारे में कुछ असंगत है? नहीं; इस तर्क के साथ समस्या यह है कि सामान्य वस्तुओं के संबंध में इसी तरह के मुद्दे पैदा होते हैं। आप एक कुर्सी के कारणों को देख सकते हैं क्योंकि आप देख सकते हैं कि बढ़ई लकड़ी से कुर्सी का निर्माण कैसे करता है, लेकिन लकड़ी किससे बनी? इससे भी बढ़कर, लकड़ी को बनाने वाले परमाणु किससे बने? कोई भी इन प्रश्नों को पूछ सकता है, इनके पूरी तरह से पर्याप्त और पूर्ण स्पष्टीकरण हो सकते हैं
लेकिन सामान्य परिस्थितियों में आगे बढ़ना संभव नहीं है। ऐसे कई तथ्य और वस्तुएं हैं जिनके लिए हमें शायद कभी अच्छी व्याख्या नहीं मिले।
यहाँ भी हार के मामले में हार के कलात्मक डिजाइन की उत्पत्ति पर विचार करें। हार एक सामान्य हार प्रतीत हुआ, जिसे एक इरादे और कलात्मकता के साथ तैयार किया गया था। यह इस सवाल का जवाब देता है कि कलात्मकता कहां से आई है। कौन (या क्या) कौशल और ज्ञान इस हार बनाने में लगा है? स्टॉर्ज़ मैक्कल (2010) का कहना है कि इस समस्या का कोई हल नहीं है। शायद कुछ तथ्यों में स्पष्टीकरण नहीं है। इस बात पर जोर देते हुए कि हर चीज का स्पष्टीकरण होना अनिवार्य है।
प्रेडेस्टिनशन विरोधाभास
स्टार ट्रेक से एक अन्य उदाहरण, जहां पूर्ववर्ति यानि प्रेडेस्टिनशन विरोधाभास का अर्थ है “एक समय लूप जिसमें एक समय यात्री जो अतीत में चला गया है वह एक घटना का कारण बनता है जो अंततः व्यक्ति के मूल भविष्य के संस्करण को अतीत में वापस जाने का कारण बनता है। वाक्यांश का यह उपयोग 1996 में स्टार ट्रेक: डीप स्पेस नाइन के एक एपिसोड में ट्रायल्स एंड ट्रिबल-एटियन शीर्षक के लिए बनाया गया था। इस वाक्यांश का उपयोग पहले केल्विनवाद और मार्क्सवाद के कुछ रूपों जैसे विश्वास प्रणालियों को संदर्भित करने के लिए भी किया गया था जो अनुयायियों को कुछ परिणामों का उत्पादन करने के लिए प्रयास करने के लिए प्रोत्साहित करते थे, जबकि एक ही समय में यह सिखाते थे कि परिणाम पूर्व निर्धारित थे। स्मिंक और मॉर्गेनस्टर्न विशेष रूप से उन परिस्थितियों को संदर्भित करने के लिए “पूर्ववर्ति विरोधाभास” शब्द का उपयोग करते हैं जिसमें एक समय यात्री अतीत में कुछ घटना को रोकने की कोशिश करने के लिए समय मे पीछे जाता है, लेकिन साथ ही उसी घटना का कारण बनने में भी मदद करता है।
भौतिकी में शब्द कॉज़ल लूप
भौतिकी के संदर्भ में कुछ सैद्धांतिक कारण लूप को पेश करने के लिए, आइए हम समय की तरह वक्र के विचार पर विचार करें। एक समय की तरह वक्र स्थान-समय के माध्यम से एक वस्तु का मार्ग है जहां वस्तु प्रत्येक अंतराल के बीच समय-समय पर कनेक्शन के साथ स्थानीय रूप से आगे रहती है। एक कारण लूप तब होता है जब किसी वस्तु का समय जैसा वक्र अपने आप वापस आ जाता है।
एक कारण लूप शुरू करने का एक तरीका इस विचार के साथ है कि ब्रह्मांड में एक लुढ़का हुआ स्थान-समय है। इस विचार के लिए सबसे अच्छा सादृश्य एक सिलेंडर है जहां अंतरिक्ष बनाने वाले आयाम सिलेंडर की धुरी हैं। यह संरचना किसी वस्तु के समय जैसी वक्र को सिलेंडर के चारों ओर लूप करने और स्वयं से मिलने देती है।


उपरोक्त छवि बताती है कि जब आइंस्टीन ने दुनिया को दुनिया की एक नई समझ के साथ प्रस्तुत किया- उनका सामान्य सापेक्षता का सिद्धांत। इस सिद्धांत में, अंतरिक्ष एक खाली शून्य नहीं है, बल्कि एक अदृश्य संरचना है जिसे स्पेसटाइम कहा जाता है। न ही अंतरिक्ष केवल एक त्रि-आयामी ग्रिड है जिसके माध्यम से पदार्थ और ऊर्जा चलती है। यह एक चार-आयामी संरचना है जिसका आकार पदार्थ और ऊर्जा की उपस्थिति से निर्धारित होता है। किसी भी द्रव्यमान (या ऊर्जा) के आसपास, स्पेसटाइम घुमावदार होता है। ग्रहों, तारों और आकाशगंगाओं की उपस्थिति अंतरिक्ष-समय के ताने-बाने को वैसे ही विकृत कर देती है जैसे कोई बड़ी गेंद चादर को विकृत कर देती है। (यह विकृति चार आयामों में होती है, इसलिए द्वि-आयामी बेडशीट एक सीमित मॉडल है। इस अवधारणा की अधिक सटीक छवि बनाने के लिए ग्रह के सभी किनारों पर इन अवसादों को देखने का प्रयास करें।) जब एक छोटा द्रव्यमान बड़े द्रव्यमान के पास से गुजरता है, यह बड़े द्रव्यमान की ओर घटता है क्योंकि स्पेसटाइम स्वयं बड़े द्रव्यमान की ओर घुमावदार होता है। छोटा द्रव्यमान किसी भी बल द्वारा बड़े द्रव्यमान की ओर “आकर्षित” नहीं होता है। छोटा द्रव्यमान बड़े द्रव्यमान के पास घुमावदार स्पेसटाइम की संरचना का अनुसरण करता है। उदाहरण के लिए, विशाल सूर्य अपने चारों ओर स्पेसटाइम को घुमाता है, एक वक्रता जो सौर मंडल के किनारों तक और उससे आगे तक पहुंचती है। सूर्य की परिक्रमा करने वाले ग्रहों को सूर्य द्वारा खींचा नहीं जा रहा है; वे सूर्य द्वारा विकृत घुमावदार स्पेसटाइम का अनुसरण कर रहे हैं।
वर्महोल-आधारित समय यात्रा भी बंद समय की तरह घटता है, जिन्न की संभावना के लिए भौतिकी कुछ गंभीर समस्याएं खड़ी करती है (ऊपर चर्चा की गई है)। उष्मागतिकी के दूसरे नियम के अनुसार, एंट्रोपी (या विकार) हमेशा समय के साथ बढ़ता है। टाइमराइडर में हार के उदाहरण पर विचार करें।
ऊष्मागतिकी के अनुसार
सामान्य परिस्थितियों में, हार की एन्ट्रापी (ऊपर चर्चा की गई) उस क्षण से बढ़ जाएगी जब क्लेयर ने हार को चुरा लिया जब हार को स्वान को दिया जा रहा था और जब तक स्वान समय यात्रा नहीं करता। अब समय यात्रा की सबसे अधिक समझ वस्तुओं की स्थिति को नहीं बदलती क्योंकि वे समय में पीछे यात्रा करती हैं। चूंकि स्वान के वापस जाने से ठीक पहले हार की एन्ट्रापी में उतनी ही मात्रा होनी चाहिए जितनी कि स्वान के अतीत में आने पर, यह एक विरोधाभास पैदा करेगा। चूंकि स्वान के वापस जाने से ठीक पहले हार की एन्ट्रापी में उतनी ही मात्रा होनी चाहिए जितनी कि स्वान के अतीत में आने पर, यह एक विरोधाभास पैदा करेगा क्योंकि स्वान के जाने से ठीक पहले हार की एन्ट्रापी, स्वान के अतीत में आने के बराबर और अधिक होती है। इस विरोधाभास का मतलब है कि जिन्न के अस्तित्व के लिए समय यात्रा मॉडल को किसी तरह से अतीत में लौटने के लिए एन्ट्रापी को कम करने के लिए जिम्मेदार होना चाहिए।
एक बड़े धमाके से उत्पन्न होने के बजाय, ब्रह्मांड एक अंतरिक्ष-समय ’डोनट’ के रूप में शुरू हुआ
भौतिकी में कारण लूप का एक और दिलचस्प उदाहरण वह परिकल्पना है जो एक बड़े धमाके से उत्पन्न होने के बजाय, ब्रह्मांड एक अंतरिक्ष-समय डोनट ’के रूप में शुरू हुआ, जहां से शेष ब्रह्मांड ब्रांच हुआ। इस सिद्धांत के लेखक जे. रिचर्ड गॉट और ली-शिन ली ने आइंस्टीन के क्षेत्र समीकरणों के वैकल्पिक समाधान के आधार पर इस सिद्धांत को तैयार किया। अंतरिक्ष-समय डोनट अनिवार्य रूप से एक कारण है, जिसमें लूप के चारों ओर बंद और खुले मार्ग होते हैं। तो अंतरिक्ष-समय के माध्यम से कुछ पथ एक लूप के रूप में मौजूद हैं, लेकिन बाकी ब्रह्मांड और इसकी सामग्री बनाने के लिए शाखाएं हैं।
कॉसल लूप्स और मल्टी-डायमेंशनल टाइम
बहु-आयामी समय को कभी-कभी समय की शाखाओं में बंटने के साथ समय की संरचना कहा जाता है और जो कारण लूप की दिलचस्प विशेषताओं को हटा देता है। यह कभी-कभी कारण लूप को बाहर रखने के लिए पेश किया जाता है। समय-यात्रा के कारण समय-सीमा बहु-आयामी समय के साथ विभाजित हो जाती है, इसलिए एक घटना इसकी पिछली शाखा के साथ एक घटना का कारण नहीं बन सकती है। यह लूप्स को अलिखित करता है और जो कुछ बचा है, वह विभाजित कारण श्रृंखलाओं की एक श्रृंखला है। इसका एक परिणाम यह है कि, यदि बहुआयामी समय सच होना था, तो इस सवाल का उत्तर कि क्या हमेशा अतीत की यात्रा में एक कारण लूप शामिल होता है, नहीं। एक समय यात्री छोरों के बजाय शाखाएं बनाता है।
क्वांटम गणना के साथ नेगेटिव डिले
1991 के एक पेपर में भौतिक विज्ञानी डेविड ड्यूश ने दिखाया कि क्वांटम गणना एक नेगेटिव डिले के साथ (समय मे पीछे यात्रा) बहुपद समय में NP की समस्याओं को हल कर सकता है। बाद में स्कॉट आरोनसन ने इस परिणाम को यह दिखाने के लिए बढ़ाया कि मॉडल का उपयोग बहुपद समय में PSPACE की समस्याओं को हल करने के लिए भी किया जा सकता है। ड्यूश ने दिखाया कि एक नेगेटिव डिले के साथ क्वांटम गणना केवल आत्म-सुसंगत समाधान पैदा करती है, और कालक्रम-उल्लंघन क्षेत्र उन बाधाओं को लगाता है जो शास्त्रीय तर्क के माध्यम से स्पष्ट नहीं हैं। 2014 में शोधकर्ताओं ने फोटॉनों के साथ ड्यूश के मॉडल को मान्य करने वाला एक सिमुलेशन प्रकाशित किया था, हालांकि, यह टॉल्क्सडॉर्फ और वर्च के एक लेख में दिखाया गया था कि ड्यूश का CTC (टाइमलाइक कर्व, या एक कारण लूप) निश्चित-बिंदु स्थिति किसी भी क्वांटम में मनमानी परिशुद्धता के लिए पूरा किया जा सकता है स्पेसकिट पर क्वांटम क्षेत्र के सिद्धांत के अनुसार वर्णित प्रणाली जहां CTCs को बाहर रखा गया है, इस पर संदेह व्यक्त करना कि क्या ड्यूश की स्थिति सामान्य सापेक्षता के अर्थ में CTCs की नकल करने वाली क्वांटम प्रक्रियाओं की विशेषता है।
स्वयंकार्यान्वित भविष्यवाणी(Self-fulfilling prophecy)
एक स्व-पूर्ति भविष्यवाणी एक ऐसी प्रक्रिया है जिसमें मूल रूप से झूठी अपेक्षा इसकी पुष्टि की ओर ले जाती है। एक स्व-पूर्ति की भविष्यवाणी में, किसी अन्य व्यक्ति या संस्था के बारे में एक व्यक्ति की अपेक्षाओं का परिणाम अंततः दूसरे व्यक्ति या संस्था के रूप में कार्य करता है जो अपेक्षाओं की पुष्टि करता है।
इस प्रकार स्व-पूर्ति भविष्यवाणी कार्य-कारण लूप का एक रूप हो सकती है। पूर्वनिर्धारण मे जरूरी नहीं कि एक अलौकिक शक्ति शामिल हो, अन्य “अचूक पूर्वाभास” तंत्र का परिणाम भी हो सकता है। अचूकता और भविष्य को प्रभावित करने से उत्पन्न समस्याओं को न्यूकोम्ब के विरोधाभास में खोजा गया है। स्व-पूर्ण भविष्यवाणी का एक उल्लेखनीय काल्पनिक उदाहरण ओडिपस रेक्स के शास्त्रीय नाटक में होता है, जिसमें ओडिपस थेब्स का राजा बन जाता है और इस प्रक्रिया में अनजाने में एक भविष्यवाणी पूरी होती है कि वह अपने पिता को मार डालेगा और अपनी माँ से शादी करेगा। भविष्यवाणी ही अपने कार्यों के लिए प्रेरणा का काम करती है, और इस प्रकार यह स्वयं पूर्ण होती है। फिल्म 12 बंदरों की भविष्यवाणी और कैसंड्रा कॉम्प्लेक्स के विषयों से काफी हद तक संबंधित है, जहां नायक जो समय में पीछे यात्रा करता है, जो बताता है कि वह अतीत को नहीं बदल सकता है।
नोविकोव आत्म-संगति सिद्धांत
सामान्य सापेक्षता कुछ सटीक समाधान बतातें हैं जो समय यात्रा की अनुमति देते हैं। इनमें से कुछ सटीक समाधान उन ब्रह्मांडों का वर्णन करते हैं जिनमें बंद समय-समान वक्र होते हैं, या विश्व रेखाएं जो स्पेसटाइम में एक ही बिंदु पर वापस जाती हैं। भौतिक विज्ञानी इगोर दिमित्रिएविच नोविकोव ने 1975 और 1983 में अपनी पुस्तकों में बंद समय के समान वक्रों की संभावना पर चर्चा की है, इस राय की पेशकश करते हुए कि समय में केवल आत्म-संगत(self-consistent) यात्राओं की अनुमति होगी। नोविकोव और कई अन्य लोगों द्वारा 1990 का एक पेपर “कॉची प्रॉब्लम इन स्पेसटाइम्स विथ क्लोज्ड टाइमलाइक कर्व्स”, से पता चलता है कि आत्म-संगति का सिद्धांत, जिसमें कहा गया है कि वास्तविक ब्रह्मांड में स्थानीय रूप से होने वाले भौतिकी के नियमों का केवल समाधान ही वे हैं जो विश्व स्तर पर आत्मनिर्भर हैं। लेखकों ने बाद में निष्कर्ष निकाला कि समय यात्रा को अनसुलझे विरोधाभासों की ओर ले जाने की आवश्यकता नहीं है, भले ही अतीत में किस प्रकार की वस्तु भेजी गई हो।
भौतिक विज्ञानी जोसेफ पोल्चिंस्की ने तर्क दिया कि समय मे पीछे भेजी गई बिलियर्ड बॉल से जुड़ी संभावित विरोधाभासी स्थिति पर विचार करके कोई भी स्वतंत्र इच्छा के प्रश्नों से बच सकता है। इस स्थिति में, गेंद को वर्महोल में इस तरह से भेजा जाता है कि यदि यह अपने कोर्स के साथ जारी रहता है तो यह अतीत में अपने पहले के स्वयं को हिट करने के लिए सही कोण पर बाहर निकल जायेगा जो इस बात की पुष्टि करेगी की, इससे यह वर्महोल में प्रवेश करने से रुक जाए। थॉर्न ने इस समस्या को “पोलचिंस्की का विरोधाभास” कहा। कैल्टेक, फर्नांडो एचेवेरिया और गुन्नार क्लिंकहैमर के दो छात्रों ने एक ऐसा समाधान खोजा, जो किसी भी तरह की विसंगतियों से बचा रहा हो।
संशोधित परिदृश्य में, गेंद भविष्य से एक अलग कोण पर उभरेगी, जिसने विरोधाभास उत्पन्न किया था और वर्महोल से पूरी तरह से दूर दस्तक देने के बजाय अपने अतीत को एक चमकदार झटका देता है। यह झटका अपने प्रक्षेपवक्र को केवल सही डिग्री से बदलता है, जिसका अर्थ है कि यह अपने छोटे स्वं को आवश्यक झटका देने के लिए आवश्यक कोण के साथ समय में वापस यात्रा करेगा। एचेवेरिया और क्लिंकहैमर ने एक से अधिक आत्म-संगत समाधान पाए, प्रत्येक मामले में टकराव के लिए थोड़ा अलग कोण। थॉर्न और रॉबर्ट फॉरवर्ड के बाद के विश्लेषण से पता चला कि बिलियर्ड बॉल के कुछ प्रारंभिक प्रक्षेपवक्र के लिए अनंत संख्या में आत्मनिर्भर समाधान हो सकते हैं।
एचेवरिया, किलिंहमर, और थॉर्न ने 1991 में इन परिणामों पर चर्चा करते हुए एक पत्र प्रकाशित किया, इसके अलावा, उन्होंने बताया कि उन्होंने यह देखने की कोशिश की थी कि क्या वे बिलियर्ड बॉल के लिए कोई प्रारंभिक शर्तें पा सकते हैं जिसके लिए कोई आत्मनिर्भर एक्सटेंशन नहीं थे, लेकिन वे ऐसा करने मे असमर्थ थे। इस प्रकार यह प्रशंसनीय है कि हर संभव प्रारंभिक प्रक्षेपवक्र के लिए आत्म-संगत एक्सटेंशन मौजूद हैं, हालांकि यह साबित नहीं हुआ है। प्रारंभिक स्थितियों पर बाधाओं की कमी केवल कालक्रम के उल्लंघन वाले कालक्रम के बाहर स्पेसटाइम पर लागू होती है; कालक्रम-उल्लंघन क्षेत्र पर बाधाएं विरोधाभासी साबित हो सकती हैं, लेकिन अभी तक यह ज्ञात नहीं है।
नोविकोव के विचारों को व्यापक रूप से स्वीकार नहीं किया गया है। विज़सर ने कारण लूप और नोविकोव के स्व-स्थिरता सिद्धांत को तदर्थ समाधान के रूप में देखा और माना कि समय यात्रा के अधिक हानिकारक प्रभाव हैं। क्रसनिकोव समान रूप से कारण लूप में कोई अंतर्निहित दोष नहीं पाता है, लेकिन सामान्य सापेक्षता में समय यात्रा के साथ अन्य समस्याओं का पता लगाता है।
निष्कर्ष और अंतिम विचार
इस लेख की शुरुआत में हमने एक ऐसे समय यात्री के बारे में चर्चा की है जो अपनी समय यात्रा करने के लिए एक संग्रहालय से टाइम मशीन चुराता है, वह समय में पीछे यात्रा करता है और अतीत में पहुंचता है, फिर यात्रा के अंत में वह टाइम मशीन उसी संग्रहालय मे दान करता है जहां से उसने चुराया था। यहां हम इस विरोधाभास के कुछ पहलुओं की दृढ़ता से जांच कर सकते हैं, लेकिन हमारे पास कई सवाल भी हो सकते हैं, इसलिए चर्चा हमेशा खुली होती है। इन सवालों के बावजूद, क्या आप यह पता लगा सकते हैं कि टाइम मशीन कहाँ से आई है? आप नहीं बता सकते और हम भी नहीं बता सकते क्योंकि यहाँ टाइम मशीन खुद कभी किसी के द्वारा नहीं बनाई गई है – यह बस मौजूद है। इस प्रकार अतीत में यात्रा करने से कॉस लूप यानि कारण लूप की संभावना बनती है, जिसमें चीजें कहीं से भी आती हैं या अप्रत्याशित रूप से निकलती हैं।
स्त्रोत
- Meyer, Ulrich. “Explaining Causal Loops.” Analysis 72 (2012): 259-264.
- Smith, Nicholas J.J. (2013). “Time Travel.” Stanford Encyclopedia of Philosophy. Retrieved June 13, 2015.
- Rea, Michael C. (2009). Arguing about Metaphysics. New York [u.a.]: Routledge. p. 204. ISBN 978-0-415-95826-4.
- Thorne, Kip S. (1994). Black Holes and Time Warps. W. W. Norton. pp. 509–513. ISBN 0-393-31276-3.
- Everett, Allen; Roman, Thomas (2012). Time Travel and Warp Drives. Chicago: University of Chicago Press. pp. 136–139. ISBN 978-0-226-22498-5.
- Smeenk, Chris; Wüthrich, Christian (2011), “Time Travel and Time Machines”, in Callender, Craig (ed.), The Oxford Handbook of Philosophy of Time, Oxford University Press, p. 581, ISBN 978-0-19-929820-4
- Ross, Kelley L. (1997). “Time Travel Paradoxes”. Archived from the original on January 18, 1998.
- Jones, Matthew; Ormrod, Joan (2015). Time Travel in Popular Media. McFarland & Company. p. 207. ISBN 9780786478071.
- Holmes, Jonathan (October 10, 2015). “Doctor Who: what is the Bootstrap Paradox?”. Radio Times.
- Krasnikov, S. (2001), “The time travel paradox”, Phys. Rev. D, 65 (6): 06401, arXiv:gr-QC/0109029, Bibcode:2002PhRvD..65f4013K, DOI:10.1103/PhysRevD.65.064013
- Lossev, Andrei; Novikov, Igor (15 May 1992). “The Jinn of the time machine: non-trivial self-consistent solutions” (PDF). Class. Quantum Gravity. 9 (10): 2309–2321. Bibcode:1992CQGra…9.2309L. DOI:10.1088/0264-9381/9/10/014. Archived from the original (PDF) on November 17, 2015. We retrieved November 16, 2015.
- Okuda, Michael; Okuda, Denise (1999). The Star Trek Encyclopedia. Pocket Books. p. 384. ISBN 0-671-53609-5.
- Erdmann, Terry J.; Hutzel, Gary (2001). Star Trek: The Magic of Tribbles. Pocket Books. p. 31. ISBN 0-7434-4623-2.
- Daniels, Robert V. (May–June 1960). “Soviet Power and Marxist Determinism.” Problems of Communism. 9: 17.
- Deutsch, David (1991). “Quantum mechanics near closed timelike lines.” Physical Review D. 44 (10): 3197–3217. Bibcode:1991PhRvD..44.3197D. DOI:10.1103/PhysRevD.44.3197. PMID 10013776.
- Aaronson, Scott (March 2008). “The Limits of Quantum Computers” (PDF). Scientific American. 298 (3): 68–69. Bibcode:2008SciAm.298c..62A. DOI:10.1038/scientificamerican0308-62.
- Martin Ringbauer; Matthew A. Broome; Casey R. Myers; Andrew G. White; Timothy C. Ralph (June 19, 2014). “Experimental simulation of closed timelike curves.” Nature Communications. 5: 4145. arXiv:1501.05014. Bibcode:2014NatCo…5.4145R. DOI:10.1038/ncomms5145. PMID 24942489.
- Tolksdorf, Juergen; Verch, Rainer (2018). “Quantum physics, fields and closed timelike curves: The D-CTC condition in quantum field theory.” Communications in Mathematical Physics. 357 (1): 319–351. arXiv:1609.01496. Bibcode:2018CMaPh.357..319T. DOI:10.1007/s00220-017-2943-5.
- Craig, William Lane (1987). “Divine Foreknowledge and Newcomb’s Paradox.” Philosophia. 17 (3): 331–350. DOI:10.1007/BF02455055.
- Dummett, Michael (1996). The Seas of Language. Oxford University Press. pp. 356, 370–375. ISBN 9780198240112.
- Dodds, E.R. (1966), Greece & Rome 2nd Ser., Vol. 13, No. 1, pp. 37–49
- Krasnikov, S. (2002), “No time machines in classical general relativity,” Classical and Quantum Gravity, 19 (15): 4109, arXiv:gr-QC/0111054, Bibcode:2002CQGra..19.4109K, DOI:10.1088/0264-9381/19/15/316
- Carroll, Sean (2004). Spacetime and Geometry. Addison Wesley. ISBN 0-8053-8732-3.
- Friedman, John; Morris, Michael S.; Novikov, Igor D.; Echeverria, Fernando; Klinkhammer, Gunnar; Thorne, Kip S.; Yurtsever, Ulvi (1990). “Cauchy problem in spacetimes with closed timelike curves.” Physical Review D. 42 (6): 1915. Bibcode:1990PhRvD..42.1915F. DOI:10.1103/PhysRevD.42.1915. PMID 10013039.
- Novikov, Igor (1983). Evolution of the Universe, p. 169: “The close of time curves does not necessarily imply a violation of causality, since the events along such a closed line may be all ‘self-adjusted’—they all affect one another through the closed cycle and follow one another in a self-consistent way.”
- Echeverria, Fernando; Gunnar Klinkhammer; Kip Thorne (1991). “Billiard balls in wormhole spacetimes with closed timelike curves: Classical theory.” Physical Review D. 44 (4): 1077. Bibcode:1991PhRvD..44.1077E. DOI:10.1103/PhysRevD.44.1077.
- Earman, John (1995). Bangs, Crunches, Whimpers, and Shrieks: Singularities and Acausalities in Relativistic Spacetimes. Oxford University Press. ISBN 0-19-509591-X.
- Nahin, Paul J. (1999). Time Machines: Time Travel in Physics, Metaphysics, and Science Fiction. American Institute of Physics. pp. 345–352. ISBN 0-387-98571-9.